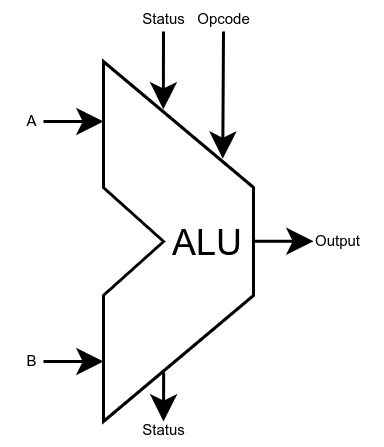
ALU
An ALU (Arithmetic Logic Unit) is a circuit for performing various integer operations. It is an essential component of any CPU.
It does not perform operations on floating point numbers, which is handled by a FPU instead.
Overview
A typical ALU has:
- 2 integer inputs.
- 1 integer output.
- 1 opcode selection input.
- 1 status input.
- 1 status output.
The status signal is used to indicate carry/overflow/...
An ALU may have more than 2 inputs. For example, fused multiply-add requires 3 input operands. Likewise, an ALU may have more than 1 output, e.g. to calculate both quotient and remainder in one operation.
Common operations
Bitwise AND, OR, XOR
These operations simply involve wiring each bit to the corresponding gate.
Shift/rotate left/right
Shifting or rotating a number by a fixed amount of bits simply involves wiring each input bit to its corresponding output bit.
Shifting by a variable amount is trickier, especially for large numbers. Using a single multiplexer will require an excessive amount of wires and gates to support every possible rotation.
A sequence multiple small multiplexers can be used, each shifting the number by x * 2y.
While this is slower it saves a lot on gates.
# Right shifter for 8 bits numbers. s4 = y[2] ? (x >> 4) : x s2 = y[1] ? (s4 >> 2) : s4 s1 = y[0] ? (s2 >> 1) : s2
Addition
An adder is composed of multiple 1-bit adders. Each of these 1-bit adders has three inputs and two outputs.
The addition of two 1-bit numbers has a 2-bit result. The high bit is called the carry. For multi-bit adder this carry is carried to the next 1-bit adder.
The LSb (out) can be calculated by XORing all three input bits together.
The MSb (carry_out) can be calculated by testing whether two or more bits are 1.
out = in_a ^ in_b ^ carry_in carry_out = (in_a & in_b) | (in_b & carry_in) | (carry_in & in_a)
Note that:
(x & z) | (y & z) = (x | y) & zx | y = (x ^ y) | (x & y)x & !x = 1
From which follows:
(in_a & in_b) | (in_b & carry_in) | (carry_in & in_a) = (in_a & in_b) | ((in_a | in_b) & carry_in) = (in_a & in_b) | (((in_a ^ in_b) | (in_a & in_b)) & carry_in) = (in_a & in_b) | ((in_a ^ in_b) & carry_in) | ((in_a & in_b) & carry_in) = (in_a & in_b) | ((in_a ^ in_b) & carry_in)
Hence we can save a few gates by using the result of in_a ^ in_b
t = in_a ^ in_b out = t ^ carry_in carry_out = (in_a & in_b) | (t & carry_in)
Faster addition
While chaining 1-bit adders is a cheap & easy way to implement a multi-bit adder, it is also slow as the signal must propagate from the lowest to the highest bit. To speed this up a carry-lookahead is used.
This lookahead computes the carry for multiple bits up, which allows using multiple small multi-bit adders in parallel.
Suppose that g = x & y and p = x ^ y, then:
c = (x & y) | ((x ^ y) & z) = g | (p & z)
Since we chain each 1-bit adder:
c1 = g0 | (p0 & c0) c2 = g1 | (p1 & c1) c3 = g2 | (p2 & c2) ...
If we fully work out c on the right side of each expression we get:
c1 = g0 | (p0 & c0) c2 = g1 | (p1 & c1) = g1 | (p1 & (g0 | (p0 & c0))) = g1 | (p1 & g0) | (p1 & p0 & c0) c3 = g2 | (p2 & c1) = g2 | (p2 & (g1 | (p1 & g0) | (p1 & p0 & c0))) = g2 | (p2 & g1) | (p2 & p1 & g0) | (p2 & p1 & p0 & c0) ...
We can group the p and g signals:
P = ... p2 & p1 & p0 G = ... (... p2 & g1) | (... p2 & p1 & g0)
And calculate the final carry signal:
C = G | (P & c0)
Addition in HDLs & simulators
Note that most HDLs & simulators already provide a component for performing addition. This component should be preferred as it can be synthesized more efficiently than a manual implementation (e.g. by using built-in adders or other components in FPGAs, such as Xilinx's CARRY4).
Subtraction
For two-complements arithmetic subtraction can be done with a - b = a + (-b).
-b is equivalent to ~b + 1, i.e. apply bitwise NOT to b and add 1.
Adding 1 can be done by setting the carry high.
Equality
The cheapest way to test for equality is by using bitwise XOR: if two numbers are equal, their XOR is 0. If not, it is nonzero. Then do a bitwise OR of all bits. If 1, the numbers are not equal.
Less Than
For unsigned arithmetic a Less Than test can be done with a subtraction and checking the carry bit.
- TODO signed arithmetic requires checking carry and high bit IIRC?
Multiplication
Division
Pitfalls
Division operation in Verilog, VHDL et al.
It may be tempting to use the division operator directly (e.g. alu_o = alu_a / alu_b).
Do not do this as it will generate a huge and slow combinatorial circuit.
Instead do each part of the division step by step, one step per clock cycle.